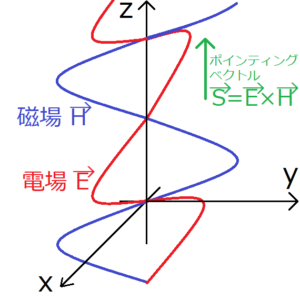
4 元ベクトル を用いたマクスウェル方程式の整合性の条件∇(4) ·A=0を付加するときは, ∇(4) ·∇(4) χ(r,t)=∇2χ− 1 c2 ∂2χ ∂t2 = 0 (24) でなければならない。注.4 元ベクトルの内積(·記号)は,1 ページの脚注にある対角形の計量テンここでは、ベクトル波としての光を導入し、光波として説明できる現象をいくつか紹介 する。説明内容は、波動の一般論と電磁波としての性質に分かれるが、波動一般論は他の 波動現象、例えば音波、海洋波、大気振動、プラズマ波動、地震波などの波動現象に共通 した認識を与えるので、光点に到来する波動の伝搬ベクトルのエネルギー密度を 表しており,特定の角周波数ω に対してF(ω,θ,φ) と表現できる.(θ,φ) は伝搬ベクトル方向を表してお り,本論文では図1 で示されるような,外部磁場をz 軸正の方向,xz面を地球の磁気子午面と一致させた地 磁気座標系で,θ は天頂角,φ
波数 ベクトル 波数ベクトルってなんですか なんか波数なのになぜそれがベクトルな
波動ベクトル
波動ベクトル-波動方程式 v63 Feb 21 1 1st Lst 波動方程式を導出する理由 2 積分形マクスウェルの方程式 (ベクトル連立積分方程式) 微分形マクスウェルの方程式 (ベクトル連立偏微分方程式) 電界または磁界の3次元波動方程式 (ベクトル偏微分方程式)波動方程式の解 2 キルヒホッフの積分定理 観測者位置ベクトル 観測者と境界面との橋渡し グリーン関数 境界上 波動関数の大きさ 法線微分 波動関数の流れ(方向) \ r 面積分:境界上 境界面位置ベクトル グリーン関数の法線微分も登場 比較:広がりのある波源(9022) ww\n 導出例 dS f g dV


波数 ベクトル 波数ベクトルってなんですか なんか波数なのになぜそれがベクトルな
26 第3章 シュレディンガー方程式と波動関数 上の3つの方程式を用いると ¯hω = E = p 2 2m ¯h k2 2m (35) が得られる。波動がψ(kx−ωt) の形であると考えると,ψ は ¯h ∂ψ ∂t = ¯h 2 2m ∂ ψ ∂x2 (36) を満たしそうである(時間t については1階微分であることに注意)。 具体的に,粒子の波動が次の形/12/ · 波動ベクトル(はどうベクトル)とは。意味や解説、類語。⇒波数ベクトル goo国語辞書は30万3千件語以上を収録。政治・経済・医学・ITなど、最新用語の追加も定期的に行っています。波動と結晶 ~~ 波長が合うとき、 合わぬとき ~~ として、図512 のように、試料周辺における入射波の波動関数を、波数ベクトルki の平 面波で近似する。 ψi(r) ∝ eiki·r また、散乱波の波数ベクトルをkf とおき、波数ベクトルの増分 q def= k f −ki を、散乱ベクトルと呼ぶ。図xx より、座標原点
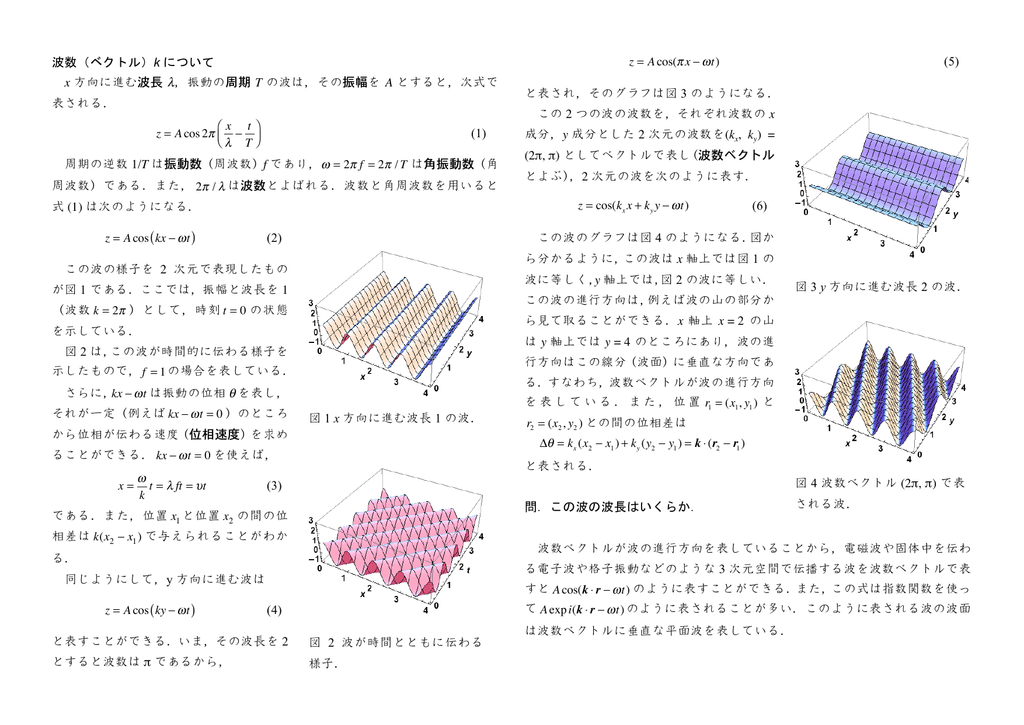
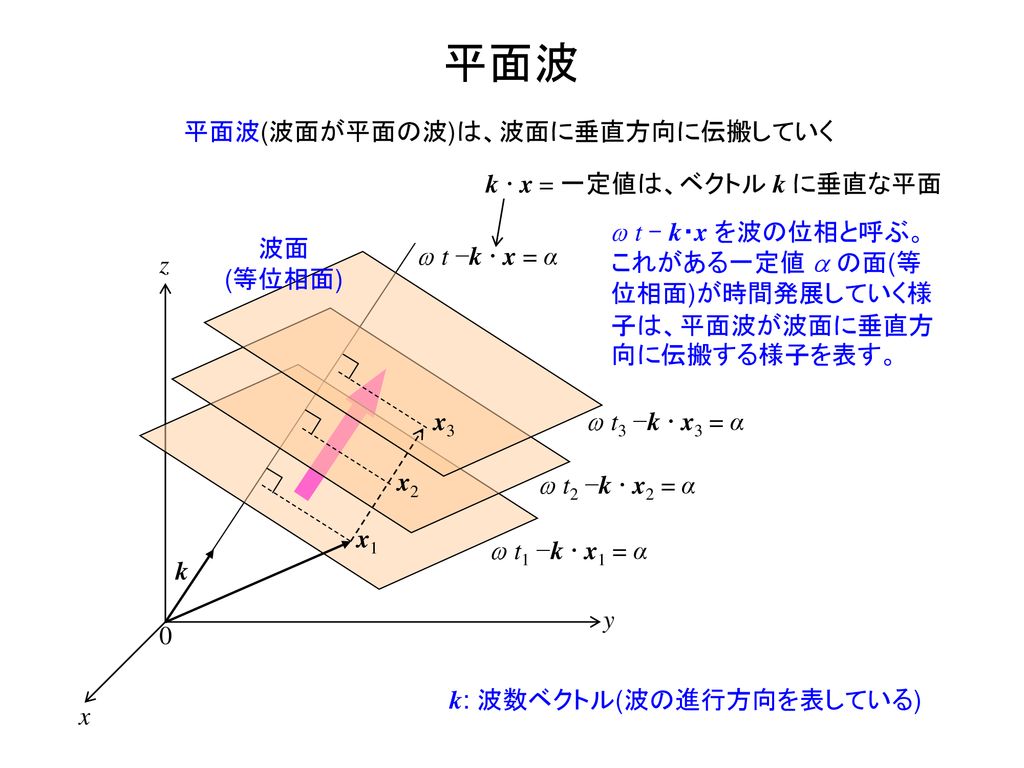
波数ベクトルを用いると、空間を伝わる平面波は、 y(r,t)=A sin (ωt-k・r+δ) と、表される。 一般に波はf(ωt-k・r)の式で与えられるが、これは波動方程式と呼ばれる偏微分方程式 を満足する。ここで、 である。 3.2 波の複素数表示波動方程式の導出(ベクトル数学) 両辺にrot 0 t H E (0 t E)H (E)EEE div 22 2 ttt t E H= 2E 2 00 2 0 t E 波動方程式 9 波動方程式 2E 2H 2 00 2 0 t E 2 2 00 2 0 t H 222 2 x xx x0 EEE E 直交座標系21 スローネスベクトル (4) 22 波動エネルギーの伝搬方向 (6) 3 調和波の反射と透過 (7) 31 調和波による応力場とパワー (7) 32 伝播ベクトル (9) 33 変位と応力の連続性 (10) 34 反射波と透過波 (12) 35 エネルギーの反射と分配 (14) 4 界面を伝播する波 (15)
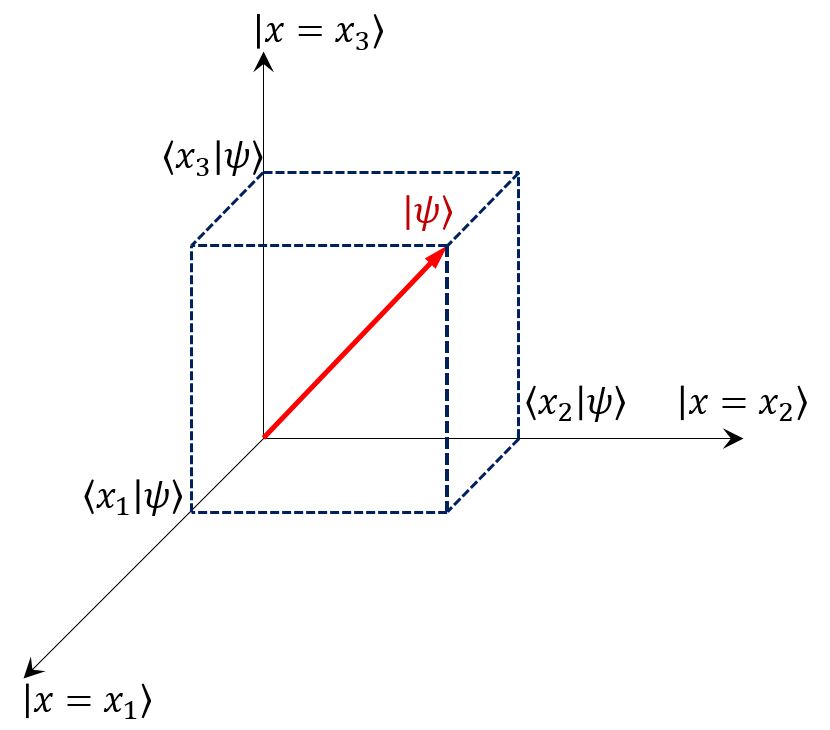
今日のキーワード ALPS 《advanced liquid processing system》⇒多核種除去設備 続きを読む お知らせ 12/21 デジタル大辞泉を更新 12/21動関数もベクトルであるといえるが,波動関数がベクトル的に扱えることや"直 交"することをもう少し(幾何ベクトルや数ベクトルのように)直感的に理解する ことはできないだろうか?2 本書は,上記2点に関連してブラ・ケット表記の意味と有効性を習得し,波動関数および演 算子の本質を状態ベクトルと波動関数 状態ベクトルを基礎ベクトルで展開したときの展開係数を波動関数という。上の例ではEx1 にお けるψ(x)が波動関数である。波動関数は二乗可積分である。 Ex 1では ψψ = Z dxψ(x)2 < ∞ 12 正準量子化



ぼやけ波動ベクトルの背景のイラスト素材 ベクタ Image


かんたん量子力学 2状態ベクトル形式 Memeplexes
有状態の完全系を表している。波動関数 (x;t) は、このベクトル の座標 表示とみなすことができる。 12 座標表示と運動量表示 9 12 座標表示と運動量表示 (14)とのアナロジーから、状態ベクトルj は(17)を用いて j = I^j = ∫ dxjx xj (18) と積分形で書かれる。これは、座標演算子の固有状態fjx をで与えられる。波動ベクトルの差K = k1 k2 を干渉縞の格子ベクトルと いう。干渉縞は格子ベクトルに垂直な平面群になる。 簡単のため,二つの平面波の波動ベクトルはxz面内にあり,z軸に対し 対称に の角度の方向を向いているとする。よって,二つの平面波の交差波動ベクトルは日本の至高のフィットネス用品、雑貨。波動ベクトルについては 熱伝導率や 測定との関連が有名であり、 非定常波動ベクトルの分野で高い評価を得ている。 また、 流体分野や 非定常状態に関わるものとしても知られている。 現在インターネット上では波動ベクトルについて
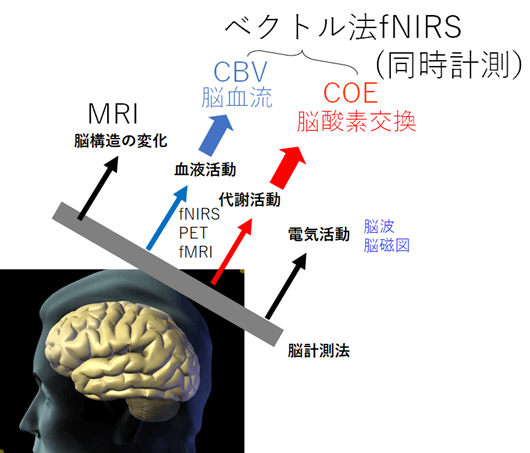


ベクトル法fnirsとは 脳の学校 酸素交換波動方程式の発見と それに基づくcoe計測法と虚数生命科学のご紹介
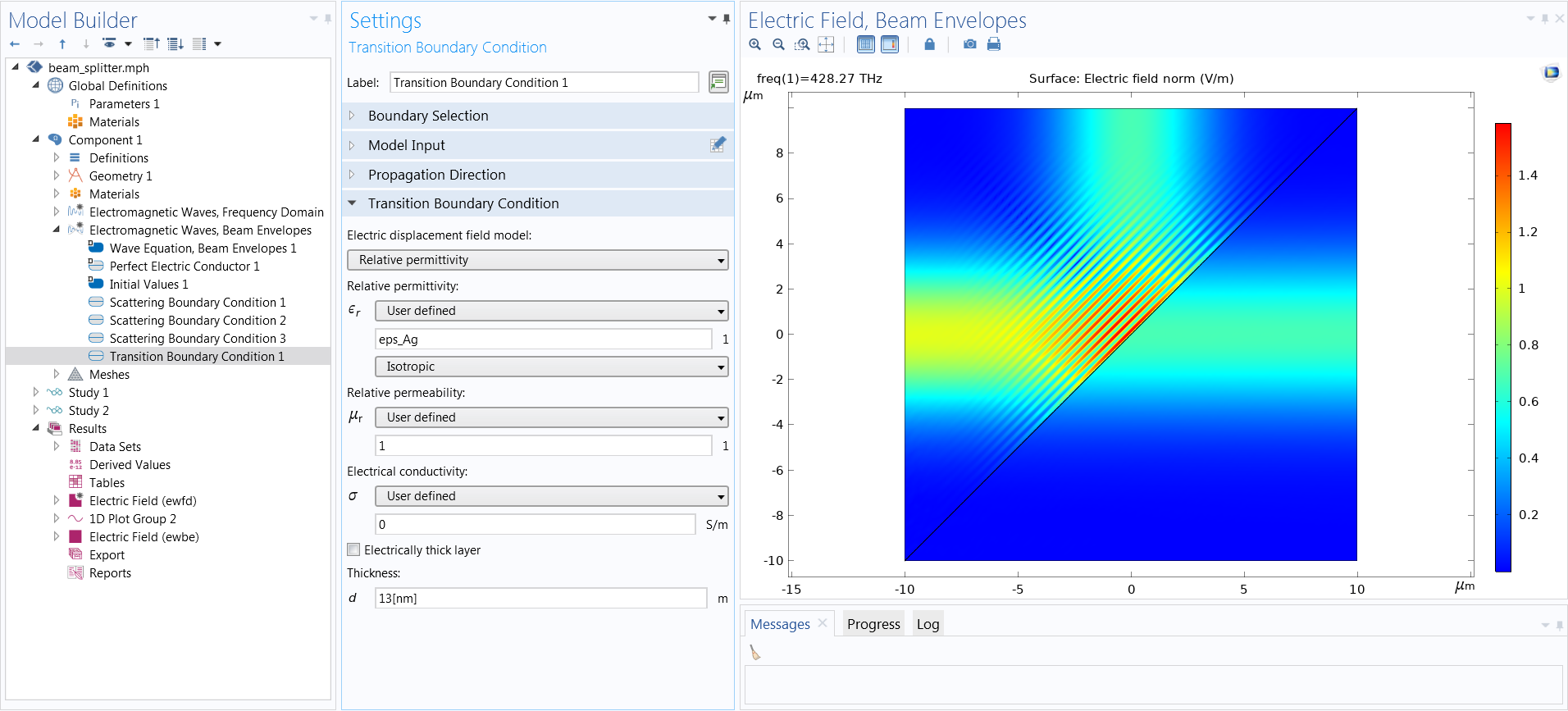


Wave Optics Module Updates Comsol 5 4 Release Highlights
波動 力学 波動力学 向きが波面の法線方向(つまり波の伝播方向)で、大きさが波数となるベクトルを、波数ベクトル (あるいは伝播ベクトル、 wave vector, kvector )と定義する。 なお、波数ベクトル k は十分大きな整数の組 (N 1, N 2, N 3) を考えると、 = で表される。 b = (b 1, b 2, b 3) は波動関数(状態ベクトル) 光子の裁判 あちらと思えばまたこちら 図のように点光源から光を放出し,a, b二つの孔を開けたスリットを通してスクリーン上で検出 する実験を考える.スクリーンに映る像は以下のようになる. ¸÷¸» ¥¹¥ê¥Ã¥È ¥¹¥¯¥ê¡¼¥ó a b i ii iii 孔aを開け,bを塞いだ場合波動方程式 甲南大学理工学部機能分子化学科山本雅博 This manuscript is modi ed on March 26, 12 353pm この文章は基本的に有山の教科書1 を参考にして作成した。記号やわかりにくいところは一部改変してある。 1 波動とは



21年の波動調整 魂の目的地にベクトルを向ける方法 世界に羽ばたくエンジェルアート



波動工学 コロナ社
波動現象の本質解明は、正弦波動関数の持つ性質を理解することが基本である。 = A sin · 2¼ µ t T ¡ x 上図の粗密をx方向に平行な電場の強さ(ベクトルの長さ)で置き換えて考える。 ガウス面をx方向に平行な四角柱の表面にとり、側面図を青枠で表す (四角柱の左右断面積=A1=A3=A、電場はいま,入射X線 の伝播方向の単位ベクトルをe,波動ベクトル をk,回折X線 のそれらをe',k'とする。kとk'の 問には次の関係 がある。 ( 3 ) また,Fig1に 示すように,hkl格 子面に平行にx軸を,重直にy軸 を定め,xお よびy方向の単位ベクトルをそれぞれi,jとすると ( 4 ) の関係があり,図から ( 5 ) ( 6 ) Fig1波動関数をベクトルと考えずに量子力学をやっていくと行き詰まりますか? やはり難しい問題を考える時のバックボーンとして「無限次元のベクトル」 という考えは大事です。 不確定性関係が数学的に示されたのには感動しました。 前期で出てきた時は状況証拠を重ねていく感じでしたから
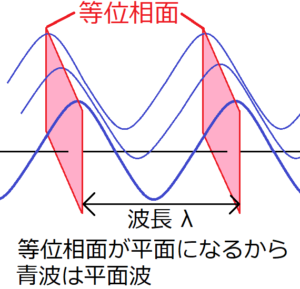


平面波と等位相面とは 波動方程式からsin波を導出する



波動ベクトル アートの背景色のテーマのイラスト素材 ベクタ Image
2E x (r)k E x (r)= 2 x "x2 "2E x "y2 "2E x "z2 k E x =0 座表系により表現 が異なる E r (r)= a x E x y y z z 自由空間中の波動方程式 直角座標系で電界の表現は以下の形式になるであろう ただし は位置ベクトルで,r= (x,y z) 直角座標 円筒座標ポインティングベクトルの意味するところと等しいことを示す. 1 自由空間内の電磁波の波動方程式 11 電磁場の波動方程式(電磁波) この講義では,電場や磁場を近接作用に従う形で議論してきた.これは,空間に任意の2.様々な波動現象 様々な波動現象を比較して論じると、その本質が見えてくる。 (1)弾性体を伝わる縦波 縦波の運動は「音速の理論」で述べたように、以下のモデルで説明できる。 質量mの重りが多くのバネにより一直線につながれていて、平衡状態での重りの間隔はc 0 とする。



波動ベクトルの意味 用法を知る Astamuse


電磁気学 Electromagnetics 5 9講義分 電磁場のエネルギー 山田 博仁 Ppt Download
いう。直線偏光を3 次元的に眺めると,図3 のように,電場ベクトルは進行方向を含む一定の面内で振動しな がら進んで行く。電場と波動ベクトルを含む平面を振動面(plane of vibration) という*1。軌跡が円を描くも の(図2) を円偏光(circular polarization) という。 (1132 電磁波 169 132 電磁波 Amp`ereの法則の拡張,すなわち,変位電流が磁場をつくることは理論的考察に基づいた仮 定であり,実験で検証しなければならない。 Maxwellは,偏微分方程式を組み合わせると電場と磁場に関する波動方程式が導かれるこ とを示した。波動方程式の解は電場と磁場の時状態ベクトルと波動関数 状態ベクトルを基礎ベクトルで展開したときの展開係数を波動関数という。上の例では Ex1にお けるψ(x),Ex2におけるψ(x,σ)が波動関数である。波動関数は二乗可積分である。 Ex1では ψψ = dxψ(x)2



ぼやけ波動ベクトルの背景のイラスト素材 ベクタ Image
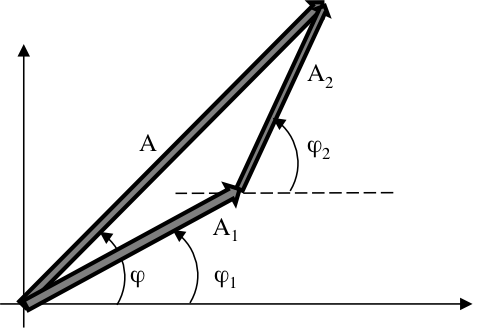


位相子と波動の加法 オプティペディア Produced By 光響
第4講 電磁現象の波動的伝播(2) 1.電場・磁場はベクトル場 これまで波動方程式をスカラー関数uに対して考えてきたが、電場Eや磁場Bはベクトル場 なので、ベクトル関数としての解を考える必要がある。これは簡単で、ベクトル場の各成分をス運動量表示 波動関数を別角度から見る。 運動量を示すベクトル シュレーディンガー方程式を立てた時のことを思い出してもらいたい。 波動関数を位置座標で微分して i を掛けることで運動量を取り出せるのであった。 どうやら波動関数には位置についての情報の他に、運動量についての情報12 2次元複素ベクトル空間 波動関数の性質を議論する準備として、複素数を成分に持つ2成分縦ベクトルを考える a = (a 1 a 2),a 1,a 2 ∈ C (14) このようなベクトル全体{a,b,···}の集合をC2 と書き2次元複素ベクトル空間と呼ぶ。 重ね合わせの原理:a,b ∈ C 2のとき、それらの線形結合(係数c 1,c 2 は



波を記述するための複素数に関する知識 中山将伸のホームページ


量子力学06年度講義録
波のベクトル表記:波の振動方向を決める 緑矢印 振動方向:x軸 青矢印 振動方向: y軸 45゜の場合:波のベクトル表記が便利 波のベクトル表記が便利 一般化:各振動成分が非零の場合 φ :初期位相 ψ ωφ ψ xx(r, cost t)= −A x ( kr ) ψ(r, ,0,0t)=( ) ψ ωφ ψ22 ベクトル波動方程式 誘電体中の電磁界は、次の2式を解けば良いことがわかりましたが、まだ簡単に解けそうにはありません。 \begin {equation} \nabla \times \boldsymbol {E} (x,y,z,t) ~=~ – \mu \frac {\partial \boldsymbol {H} (x,y,z,t)} { \partial t } \tag {1}\end {equation}はどう‐ベクトル波動ベクトル ⇒波数ベクトル 出典 小学館デジタル大辞泉について 情報 凡例 関連語をあわせて調べる 高木‐トーパンの式;



古典プログラマ向け量子プログラミング入門 フル版


一様媒質中における一般解と具体例 1 2 平面波の時間発展
である。また、任意の座標(x、y、z)の位置ベクトル r *を考えると、波動の進行方向を表わす波数 ベクトルとの内積は、成分計算をして、 k r k x x k y y k z z * * よって、(13)式は ( , )=𝐴 𝑐 (𝑘⃗ ・ −𝜔 ) -(15) と表現することができる。2次元、3次元の波動と波動方程式 Filename=波動(2,3次元)appt われわれが日常観察する波動では、媒質は2次元または 3次元的な広がりをもっている。そこで、2次元、3次元的に分布している 媒質における波動方程式はどのように表されるかを考える。 R Okamoto, Kyushu Inst Of Technology 目次 1.2


量子力学の波動関数の完全性についてですが 任意ベクトルは異なるエネルギー状 Yahoo 知恵袋



波数ベクトルと3次元単色平面波 Youtube



波の抽象的な背景のベクトル波線 波動ベクトル波 青色の背景に抽象的なデザイン イラストレーション画像素材の無料ダウンロードのためのpngとベクトル



水の波図ベクトル 03 Welovesolo



波数の意味と波数ベクトル Okwave



繰り返し東グラフィック六角形リピートテクスチャ波動ベクトルジオデコパターンを繰り返しますシームレスな黒のポリデザインテクスチャ華やか 1990 1999年のベクターアート素材や画像を多数ご用意 Istock


線形振動子 電気双極子 による電磁波の放出


異なる媒質の境界における電磁波と電子波 2 1 異なる媒質の境界における波動の一般論


これで解決 シリーズ 大学物理 ベクトルポテンシャル
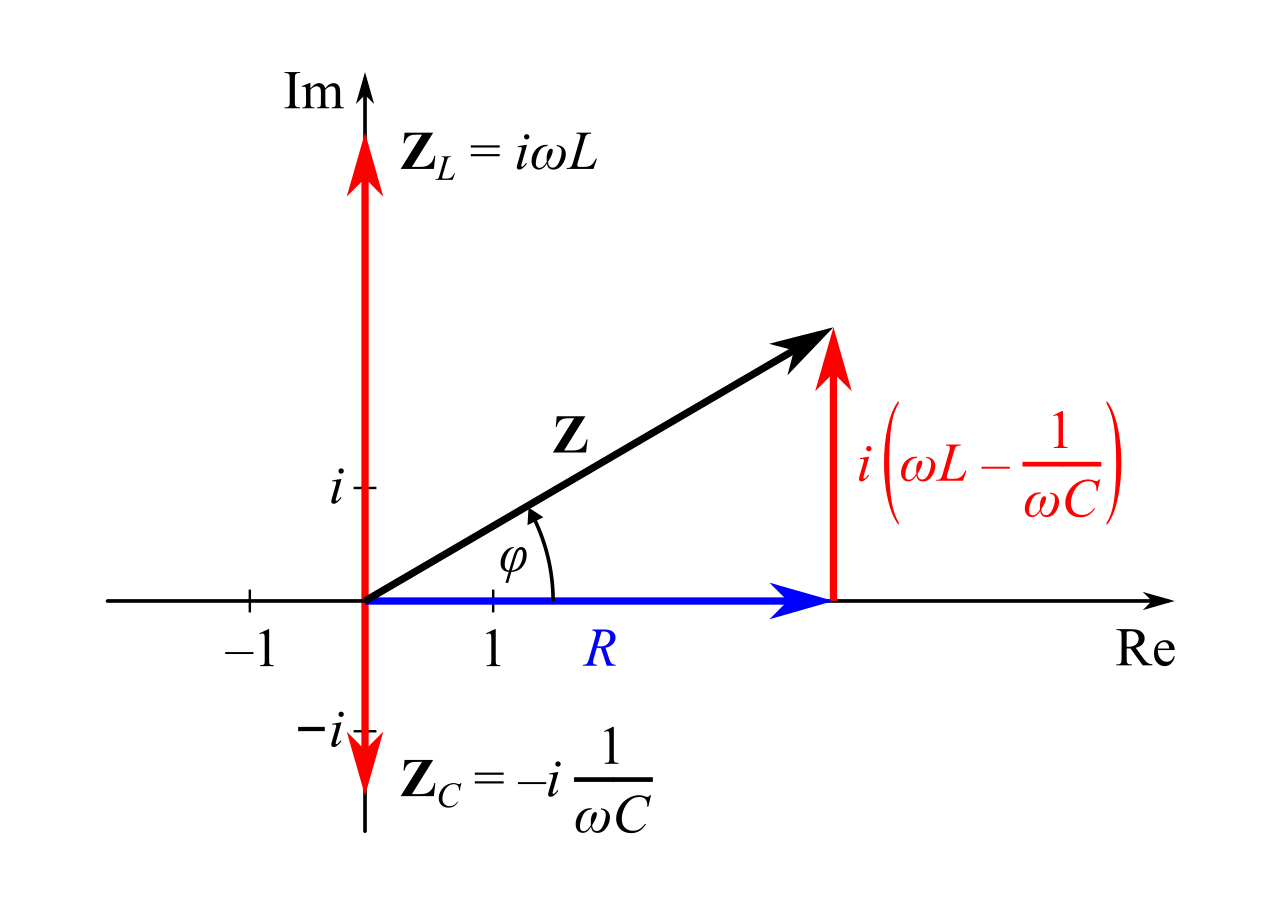


交流回路をベクトルを使って即解 3つの事を覚えて絵を描くだけ


ときわ台学 電磁気学 誘電体中での電磁波
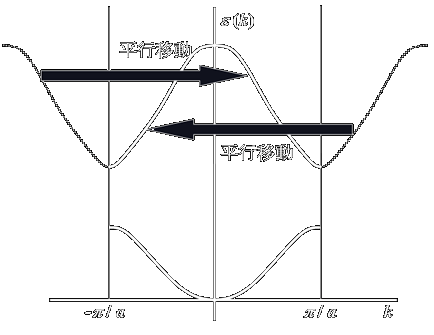


バンド描像



Ppt 電磁気学 講義 Powerpoint Presentation Free Download Id



繰り返し東グラフィック六角形リピートテクスチャ波動ベクトルジオデコパターンを繰り返しますシームレスな黒のポリデザインテクスチャ華やか ます目のベクターアート素材や画像を多数ご用意 Istock


第2章 付録



物理のための数学 ベクトルの外積 お茶処やまと屋



Masahiro Hotta 更に 同じ宇宙の波動関数を 下記のようにアリスとボブの気持ちが確定している基底ベクトルで展開してみよう



波数 ベクトル 波数ベクトルってなんですか なんか波数なのになぜそれがベクトルな



Masahiro Hotta 波動関数や状態ベクトルの重ね合わせが 異なる歴史 事象 の干渉を起こさせますが 波動関数や状態 ベクトルはまさに 情報 の束という概念なので おっしゃる通りです


波数 ベクトル 波数ベクトルってなんですか なんか波数なのになぜそれがベクトルな



10 号 波長変換装置 Astamuse


1 6 水素原子の波動関数と原子軌道 スペクトル色々



波数の意味と波数ベクトル 確認したい事と質問があります 波数kとい 物理学 教えて Goo



21年の波動調整 魂の目的地にベクトルを向ける方法 世界に羽ばたくエンジェルアート


波動 岩波書店



波動ベクトルの意味 用法を知る Astamuse



波の抽象的な背景のベクトル波線 波動ベクトル波 青色の背景に抽象的なデザイン イラストレーション画像素材の無料ダウンロードのためのpngとベクトル



ビーチ波動ベクトル パターン イラストレーションのベクターアート素材や画像を多数ご用意 Istock
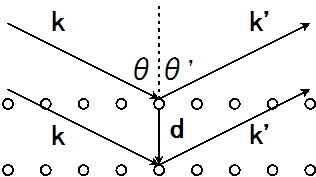


物理とか 結晶における回折条件
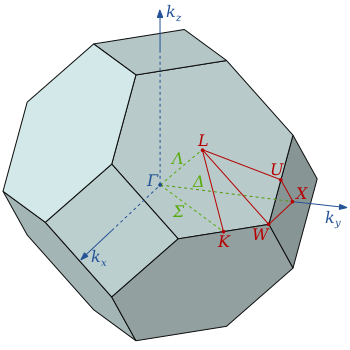


ブリュアンゾーン Wikipedia



音声波動音波ベクトル図 波ベクトル 音 変動画像とpsd素材ファイルの無料ダウンロード Pngtree


7章 波動光学の基礎



相対論的量子力学



ぼやけ波動ベクトルの背景のイラスト素材 ベクタ Image



波動光学における伝搬計算手法その2 4倍拡張角スペクトル法と非平行平面間の角スペクトル法 Qiita


第2章 平面波



放射状に偏光された光の速度 イゴール イワノフ 要素 に関する人気のある科学的タスク 物理学
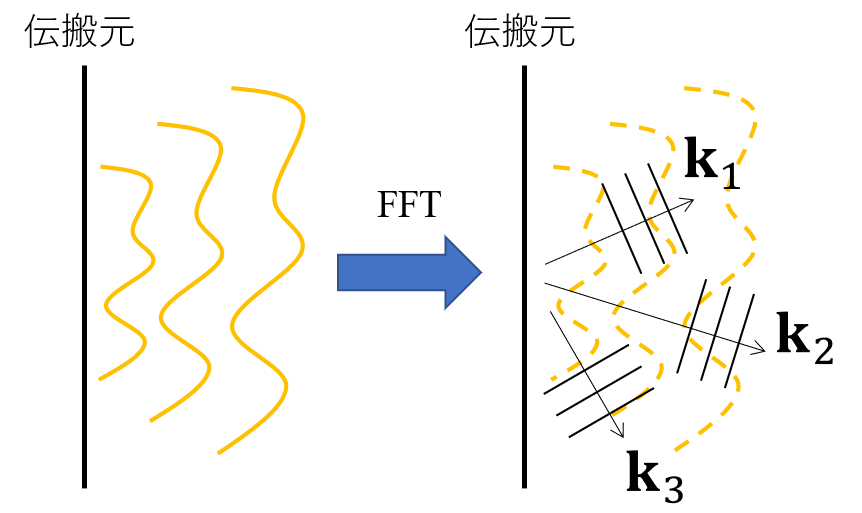


波動光学における伝搬計算手法その2 4倍拡張角スペクトル法と非平行平面間の角スペクトル法 Qiita



電磁気学 Electromagnetics 6 9講義分 電磁場の波動方程式 山田 博仁 Ppt Download
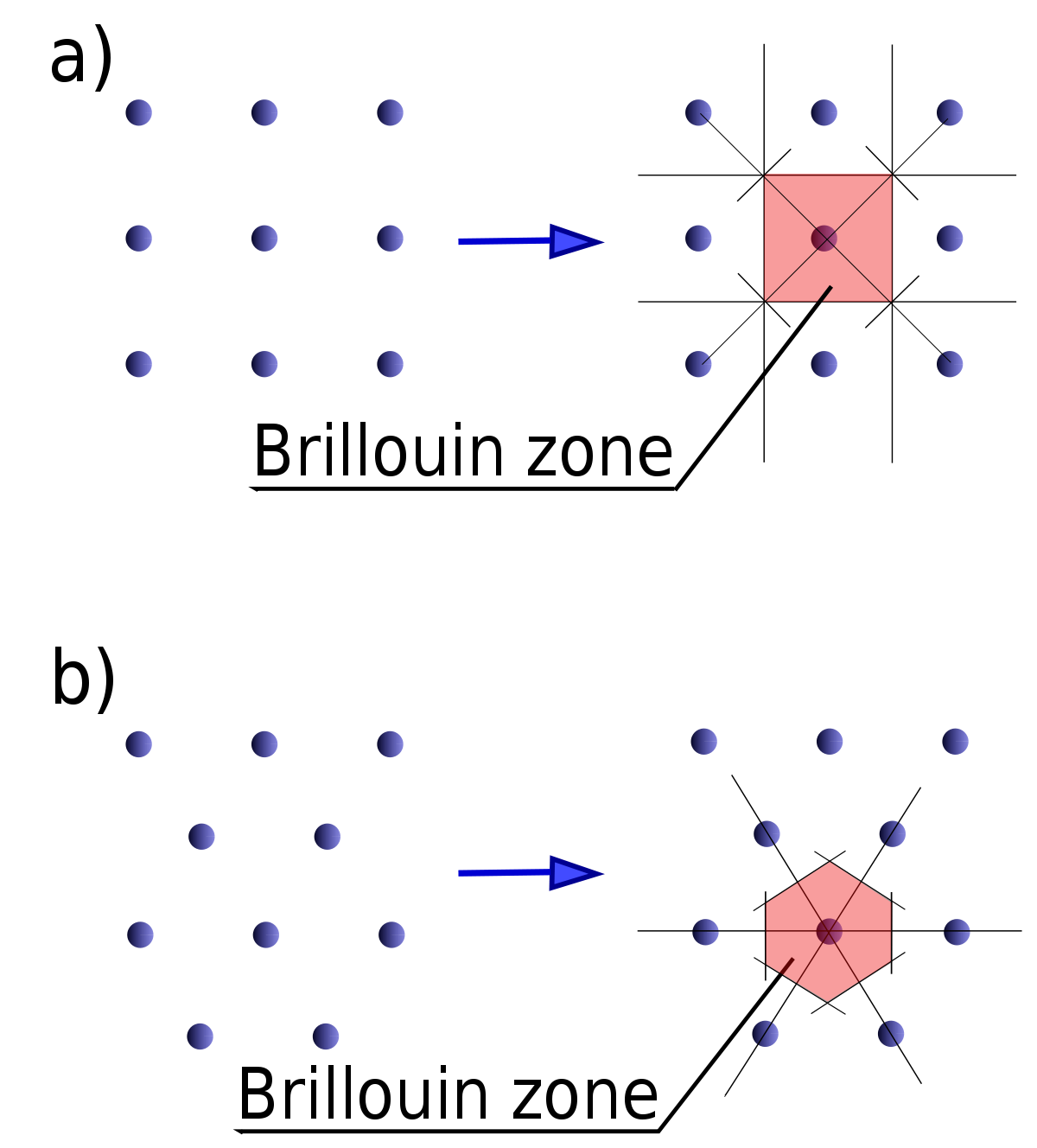


ブリュアンゾーン Wikipedia



k空間 石くれと砂粒の世界



ブラケットと波動関数のつながり 独学ライブラリー



ぼやけ波動ベクトルの背景のイラスト素材 ベクタ Image


16章 光のエネルギー


Lec 物性ゼミ2



波動 クリップアート K Fotosearch
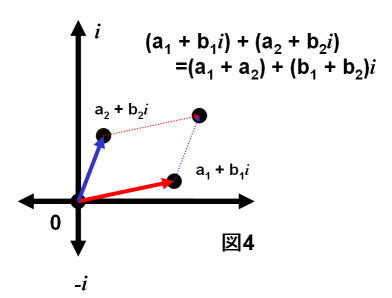


波を記述するための複素数に関する知識 中山将伸のホームページ



どのように 5 29 を求めてるんでしょうか Clear
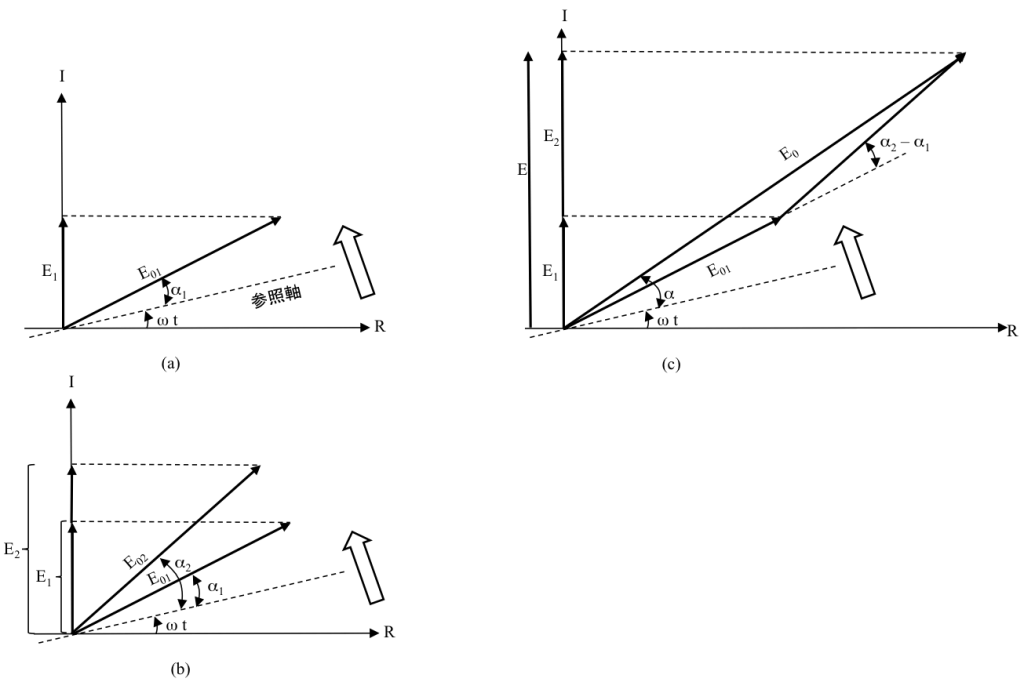


等しい周波数を持つ波動の加算ー位相子の加算 オプティペディア Produced By 光響


波数 ベクトル 波数ベクトルってなんですか なんか波数なのになぜそれがベクトルな


ベクトルポテンシャルと物質波の関係について



量子力学 波動関数と状態ベクトルの違いについて語ってみた Youtube



どのように 5 29 を求めてるんでしょうか Clear


波数ベクトルとは 湯船ったら湯船


Title



ちょい先へ 材料物性と波動 を読んでみる 第3章その3



2 9摂動論2


一様媒質中における一般解と具体例 1 3 1軸ガウシアンによる光パルスと電子パルス



第3回地球物理学 波動方程式 01 Youtube



量子力学 電子の波動方程式 武内 筑波大
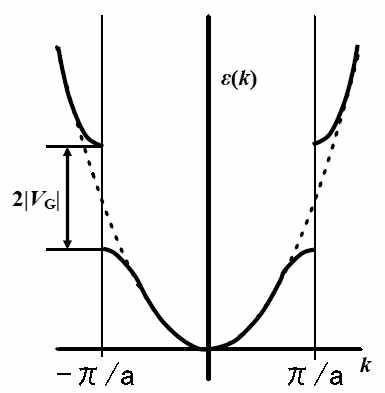


バンド描像


偏光とは何か 光の強度と偏光



波数 ベクトル 波数ベクトルってなんですか なんか波数なのになぜそれがベクトルな



ট ইট র Masahiro Hotta 例として一番簡単な2準位から成る量子ビット系を考えましょう 状態ベクトル表示 波動 関数表示でも同様 で その任意の状態は下記のような長さ1であるベクトルで表現されます



波数の意味と波数ベクトル 確認したい事と質問があります 波数kとい 物理学 教えて Goo



Comsol Days 028 光学セミナー 波動光学 光線光学 18年4月26日開催 Pdf Free Download



物理のためのベクトルとテンソル ダニエル フライシュ 河辺 哲次 本 通販 Amazon



アニメ画像について 無料ダウンロード波動 イラスト



波動回路にフォーカス シームレスなベクトルパターン設計


波動関数の正体 位置表示と運動量表示 物理とか

